2023년 11월 16일에 실시한 대학수학능력시험 수학 공통과목 단답형 문항(16번-22번) 풀이입니다. 문제의 저작권은 한국교육과정평가원에 있습니다. 풀이의 저작권은 이 블로그 주인에게 있습니다. (이메일: tomie@ly4i.com)
풀이에 틀린 것이 있을 수 있어요ㅜㅜ 읽을 때 조심! 또 조심!
문제 16. 다음 방정식을 만족시키는 실수 \(x\)의 값을 구하시오. [3점] \[3^{x-8} = \left( \frac{1}{27}\right) ^x .\]
풀이
밑이 \(1\)보다 큰 지수함수가 일대일 함수라는 사실을 사용하자. \[\begin{aligned} 3^{x-8} &= \left( 3^{-3} \right)^x ,\\[6pt] 3^{x-8} &= 3^{-3x} ,\\[6pt] x-8 &= -3x ,\\[6pt] 4x-8 &= 0 ,\\[6pt] \therefore \,\, x &= 2. \end{aligned}\]
문제 17. 함수 \(f(x)=(x+1)(x^2 + 3)\)에 대하여 \(f ' (1)\)의 값을 구하시오. [3점]
풀이
곱 미분법을 사용하자. \[\begin{aligned} f ' (x) &= (x^2 + 3 ) + 2x(x+1) \\[6pt] &= x^2 +3 + 2x^2 +2x \\[6pt] &= 3x^2 +2x +3 ,\\[6pt] f ' (1) &= 3+2+3 = 8. \end{aligned}\]
문제 18. 두 수열 \(\left\{ a_n \right\} ,\) \(\left\{ b_n \right\}\)에 대하여 \[\sum_{k=1}^{10} a_k = \sum_{k=1}^{10} (2b_k - 1) ,\quad \sum_{k=1}^{10} (3a_k + b_k ) = 33\] 일 때, \[\sum_{k=1}^{10} b_k\] 의 값을 구하시오. [3점]
풀이
\(k=1\)일 때부터 \(k=10\)일 때까지 두 수열의 합을 각각 \[\sum_{k=1}^{10} a_k = A ,\quad \sum_{k=1}^{10} b_k = B\] 라고 하자. 그러면 문제의 조건에서 제시된 두 등식은 다음과 같은 연립방정식으로 표현된다. \[\left\{ \begin{array}{l} A = 2B - 10 \\[6pt] 3A+B = 33 \end{array} \right.\] 연립방정식에서 처음 식이 \(A\)에 대하여 풀린 식이다. 두 번째 식의 \(A\)를 \(2B-10\)으로 바꾸면 \[3(2B-10) +B = 33\] 이다. 이 방정식을 풀면 다음과 같다. \[\begin{gathered} 6B - 30 +B =33 ,\\[6pt] 7B = 63 ,\\[6pt] B = 9 \end{gathered}\] 그러므로 구하는 합은 \[\sum_{k=1}^{10} b_k = 9 .\]
문제 19. 함수 \(f(x)\)가 다음과 같다. \[f(x) = \sin \left( \frac{\pi}{4} x \right) .\] 이때, 부등식 \[f(2+x) f(2-x) < \frac{1}{4}\] 을 만족시키는 모든 자연수 \(x\)의 값의 합을 구하시오. [3점]
풀이
삼각함수의 덧셈 정리를 사용하자. \[\begin{aligned} f(2+x) &= \sin\left( \frac{\pi}{2} + \frac{\pi}{4} x \right) \\[6pt] &= \sin \frac{\pi}{2} \cdot \cos\frac{\pi}{4} x + \cos\frac{\pi}{2} \cdot\sin \frac{\pi}{4} x \\[6pt] &= \cos \frac{\pi}{4} x ,\\[6pt] f(2-x) &= \sin\left( \frac{\pi}{2} - \frac{\pi}{4} x \right) \\[6pt] &= \sin\frac{\pi}{2} \cdot \cos\left( - \frac{\pi}{4} x\right) + \cos \frac{\pi}{2} \cdot\sin \left( - \frac{\pi}{4} x \right) \\[6pt] &= \cos \frac{\pi}{4} x \end{aligned}\] 이므로, 문제의 방정식은 다음과 같이 쓸 수 있다. \[\left\{ \cos \frac{\pi}{4} x \right\} ^2 < \frac{1}{4}\] 즉 \[- \frac{1}{2} < \cos \frac{\pi}{4} x < \frac{1}{2} .\] \(0 < x < 16\)인 범위에서 이 부등식의 해는 \[ \frac{4}{3} < x < \frac{8}{3} \quad\text{or}\quad \frac{16}{3} < x < \frac{20}{3} \quad\text{or}\quad \frac{28}{3} < x < \frac{32}{3} \quad\text{or}\quad \frac{40}{3} < x < \frac{44}{3} \] 이다. 이 범위에 있는 자연수 \(x\)는 \[2,\,\,6,\,\,10,\,\,14\] 이다. 이 자연수들의 합은 \(32\)이다.
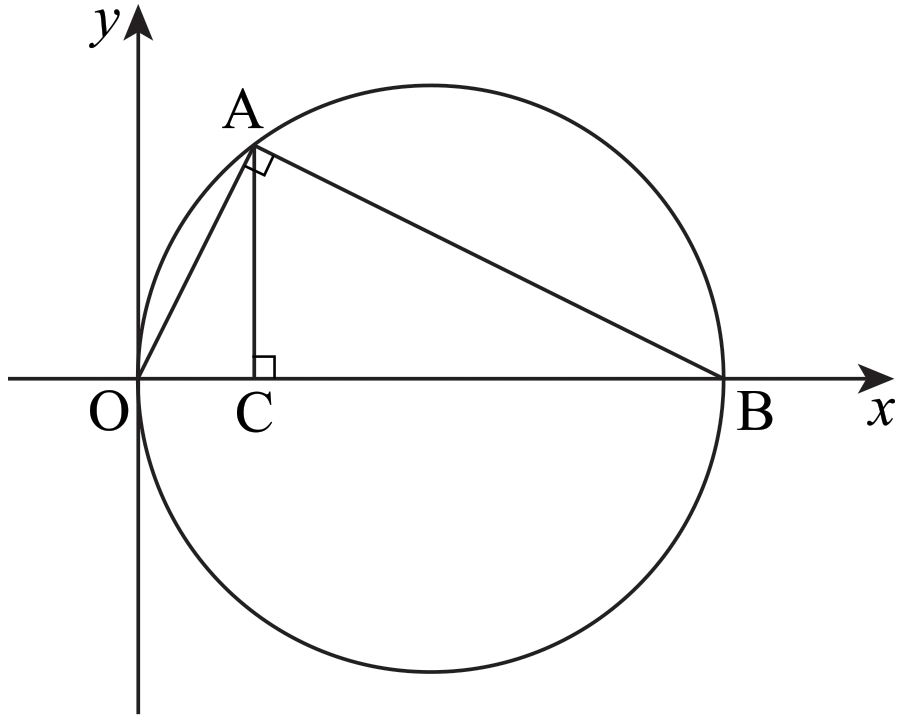
문제 20. \(a > \sqrt{2}\)인 실수 \(a\)에 대하여 함수 \(f(x)\)를 \[f(x) = -x^3 +ax^2 +2x\] 라 하자. 곡선 \(y=f(x)\) 위의 점 \(\mathrm{O} (0,\,\,0)\)에서의 접선이 곡선 \(y=f(x)\)와 만나는 점 중 \(\mathrm{O}\)가 아닌 점을 \(\mathrm{A}\)라 하고, 곡선 \(y=f(x)\) 위의 점 \(\mathrm{A}\)에서의 접선이 \(x\)축과 만나는 점을 \(\mathrm{B}\)라 하자. 점 \(\mathrm{A}\)가 선분 \(\mathrm{OB}\)를 지름으로 하는 원 위의 점일 때, \(\overline{\mathrm{OA}} \times \overline{\mathrm{AB}}\)의 값을 구하시오. [4점]
풀이
우선 점 \(\mathrm{A}\)의 위치를 구하자. \[\begin{aligned} f ' (x) &= -3x^2 + 2ax + 2 ,\\[6pt] f ' (0) &= 2 ,\\[6pt] f (0) &= 0 \end{aligned}\] 이므로 점 \(\mathrm{O}\)에서 곡선에 접하는 접선의 방정식은 \(y=2x\)이다. 이 접선의 방정식과 \(y=f(x)\)를 연립하여 풀면 \[\begin{aligned} -x^3 +ax^2 +2x &= 2x ,\\[6pt] -x^3 +ax^2 &= 0 ,\\[6pt] x^2 (a-x) &= 0 , \\[6pt] x &= a \end{aligned}\] 이다. 점 \(\mathrm{A}\)의 \(x\)좌표가 \(a\)이고, 점 \(\mathrm{A}\)가 직선 \(y=2x\) 위에 있으므로, 점 \(\mathrm{A}\)의 좌표는 다음과 같다. \[\mathrm{A} (a,\,\,2a )\] 다음으로 점 \(\mathrm{A}\)에서 곡선 \(y=f(x)\)에 접하는 접선의 방정식을 구하자. \[f ' (a) = -3a^2 + 2a^2 +2 = -a^2 + 2\] 이므로, 구하는 접선의 방정식은 다음과 같다. \[y = (-a^2 + 2 )(x-a) +2a\] 즉 \[y = (-a^2 +2)x + a^3 .\] 이 식에 \(y=0\)을 대입하면 \[(-a^2 + 2)x = -a^3\] 이므로 \[x = \frac{a^3}{a^2 - 2}\] 이다. 그러므로 점 \(\mathrm{B}\)의 좌표는 다음과 같다. \[\mathrm{B} \left( \frac{a^3}{a^2 -2} ,\,\, 0 \right).\] 점 \(\mathrm{A}\)에서 \(x\)축에 내린 수선의 발을 \(\mathrm{C}\)라고 하자. 그러면 점 \(\mathrm{C}\)는 선분 \(\mathrm{OB}\) 위에 있다.
직각삼각형의 닮음 성질에 의하여 다음과 같은 비례식을 얻는다. \[\begin{gathered} \overline{\mathrm{OC}} : \overline{\mathrm{AC}} : \overline{\mathrm{OA}} = 1:2:\sqrt{5} ,\\[6pt] \overline{\mathrm{OA}} : \overline{\mathrm{AB}} : \overline{\mathrm{OB}} = 1:2:\sqrt{5} . \end{gathered}\] 그러므로 \[\begin{aligned} \overline{\mathrm{OA}} &= \overline{\mathrm{OB}} \times \frac{1}{\sqrt{5}} = \frac{a^3}{\sqrt{5} (a^2 - 2)} ,\\[6pt] \overline{\mathrm{AB}} &= 2 \times \overline{\mathrm{OA}} = \frac{2a^3}{\sqrt{5} (a^2 -2 )} \end{aligned}\] 이다. 한편 \[a = \overline{\mathrm{OC}} = \overline{\mathrm{OA}} \times \frac{1}{\sqrt{5}} = \frac{a^3}{5(a^2 - 2)}\] 이므로 \[a = \frac{a^3}{5(a^2 - 2 )}\] 이며, 이 등식을 \(a^2\)에 대하여 풀면 \[a^2 = \frac{5}{2}\] 이다. 그러므로 \[\begin{aligned} \overline{\mathrm{OA}} \cdot \overline{\mathrm{AB}} &= \frac{a^3}{\sqrt{5} (a^2 - 2)} \times \frac{2a^3}{\sqrt{5} (a^2 - 2)} \\[6pt] &= \frac{2 (a^2 )^3}{5 (a^2 - 2)^2} \\[6pt] &= \frac{ 2 \times \left( \frac{5}{2}\right)^3 }{ 5\times \left( \frac{5}{2} - 2 \right)^2 } \\[6pt] &= 25. \end{aligned}\]
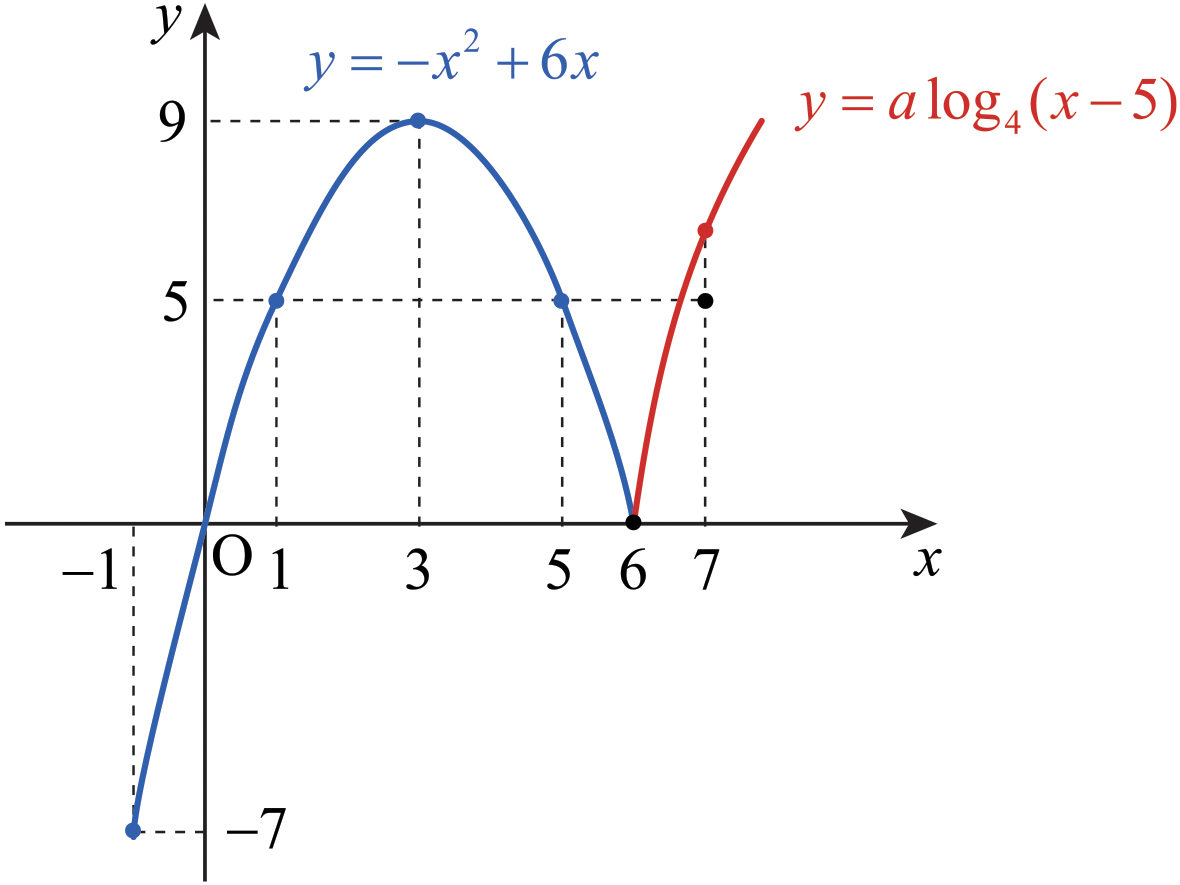
문제 21. 양수 \(a\)에 대하여, \(x\ge -1\)에서 정의된 함수 \(f(x)\)는 \[f(x) = \left\{ \begin{array}{ll} -x^2 +6x \quad & (-1 \le x < 6 ) \\[6pt] a \log_4 (x-5) \quad & (x \ge 6 ) \end{array} \right.\] 이다. \(t \ge 0\)인 실수 \(t\)에 대하여 닫힌구간 \([t-1 ,\,\,t+1]\)에서의 \(f(x)\)의 최댓값을 \(g(t)\)라고 하자. 구간 \([0,\,\,\infty )\)에서 함수 \(g(t)\)의 최솟값이 \(5\)가 되도록 하는 양수 \(a\)의 최솟값을 구하시오. [4점]
풀이
\(-1 \le x \le 6\)일 때 \(y=f(x)\)의 그래프는 이차함수의 그래프이고, 위쪽으로 볼록하다. 그리고 \(x\)의 값이 \(-1,\) \(1,\) \(3,\) \(5,\) \(6\)일 때 함숫값은 다음과 같다. \[f(-1) = -7 ,\,\, f(0) = 0 ,\,\, f(1) = 5 ,\,\, f(3) =9 ,\,\, f(5) = 5 ,\,\, f(6) =0.\] 특히 점 \((3,\,\,9)\)는 이 포물선의 꼭짓점이다.
\(x \ge 6\)일 때 \(y=f(x)\)의 그래프는 점 \((6,\,\,0)\)에서 시작하여 오른쪽 위를 향하는 곡선이다.
길이가 \(2\)인 닫힌구간 \([t-1 ,\,\, t+1]\)에서 \(f(x)\)의 최댓값이 \(g(t)\)라는 점을 고려하자. \(t\)의 값이 \(0\)에서 시작하여 \(5\)까지 커지는 동안, 함수 \(g\)의 값은 \(g(0) = 5\)에서 시작하여 점점 커지다가 \(g(2) = 9\)에 다다르고, \(g(4) = 9\)까지 상수인 상태로 있다가 그 뒤로 작아져서 \(g(5)=f(4)\)에 이른다. \(t\)의 값이 \(5\)와 \(7\) 사이에 있을 때는 \(g(t)\)의 값은 \(f(t-1)\)의 값과 \(f(t+1)\)의 값 중에서 더 큰 값을 취한다. \(t\)의 값이 \(7\)보다 크면 \(g(t) = f(t+1)\)이다.
그러므로 \(t \ge 0\)인 구간에서 \(g(t)\)의 최솟값이 \(5\)가 되려면 \(f(7)\)의 값이 \(5\) 이상이 되어야 한다. 즉 \[f(7) = a \log_4 2 = \frac{1}{2} a \ge 5\] 이므로, 이 부등식을 풀면 \(a\ge 10\)이다. 그러므로 문제의 조건을 만족시키는 \(a\)의 최솟값은 \(10\)이다.
문제 22. 함수 \(f(x)\)는 최고차항의 계수가 \(1\)인 삼차함수이다. 또한 \[f(k-1)f(k+1) < 0\] 을 만족시키는 정수 \(k\)가 존재하지 않는다. \[f ' \left( - \frac{1}{4} \right) = - \frac{1}{4} ,\quad f ' \left( \frac{1}{4} \right) < 0\] 일 때, \(f(8)\)의 값을 구하시오. [4점]
풀이
\(f(x)\)가 최고차항이 \(1\)인 삼차함수이므로, \(y=f(x)\)는 모든 구간에서 순증가하거나, 또는 서로 다른 두 극값을 가진다. 두 번째 경우 \(f\)가 극댓값을 갖는 점을 \(x=\alpha\)라고 하고 \(f\)가 극솟값을 갖는 점을 \(x=\beta\)라고 하면 \(\alpha < \beta\)이며, \(f\)는 닫힌구간 \([\alpha ,\,\, \beta ]\)에서 순감소한다. \(x=-\frac{1}{4}\)일 때와 \(x=\frac{1}{4}\)일 때 모두 \(f\)의 미분계수가 음수이므로, 함수 \(f\)는 \(-\frac{1}{4}\)과 \(\frac{1}{4}\)을 모두 원소로 갖는 닫힌구간에서 순감소한다. 즉 \(\alpha < -\frac{1}{4} < \frac{1}{4} < \beta\)이다.
부등식 \(f(k-1)f(k+1) < 0\)을 만족시키는 정수 \(k\)가 존재하지 않으려면 방정식 \(f(x)=0\)은 연속한 정수근 \(2\)개를 가져야 하며, 다른 한 근은 연속한 두 정수근 중 하나로부터 \(1\) 이하의 거리를 유지해야 한다. 그런데 \(f\)가 \(0\)을 안쪽 점으로 가지는 구간에서 한 순감소하므로, \(x=0\)은 방정식 \(f(x)=0\)의 근 중 하나이다. 왜냐하면 방정식 \(f(x)=0\)의 세 근 중 하나는 \(\alpha\) 이하이고, 하나는 \(\alpha\) 이상 \(\beta\) 이하이며, 하나는 \(\beta\) 이상이기 때문이다. 이 상황에서 세 근 중 두 개가 연속한 정수가 되려면 \(x=0\)이 반드시 한 근이 되어야 한다.
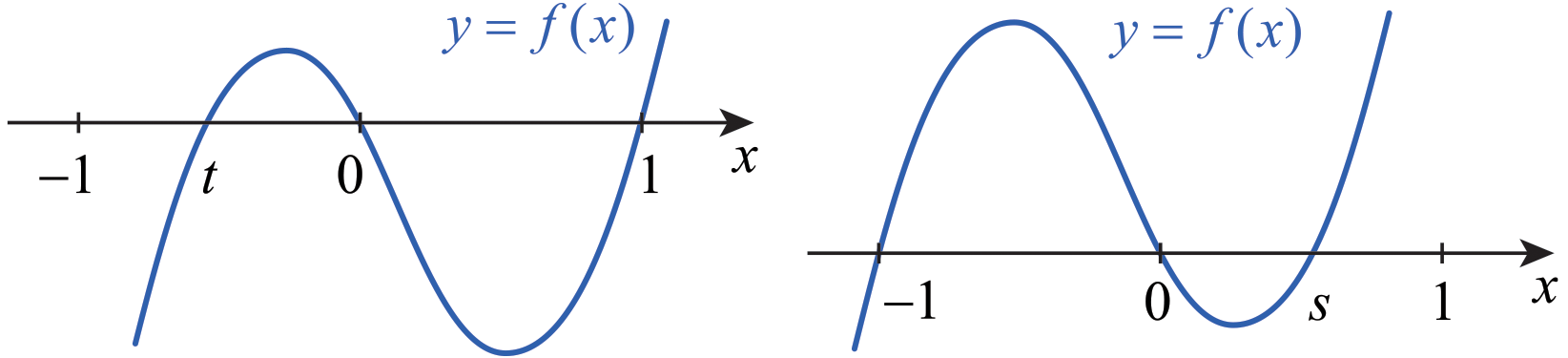
이제 방정식 \(f(x)=0\)의 근의 위치에 따라 두 가지 경우를 생각하자. 아래 그림을 보자.
(1) 첫 번째는 방정식 \(f(x)=0\)의 근이 \(x=t ,\) \(x=0 ,\) \(x=1\)이고, \(-1 \le t \le 0\)인 경우이다. 이때 \(t\)가 문제의 조건을 모두 만족시킬 수 있는지 살펴보자. \[\begin{aligned} f(x) &= x(x-1)(x-t) \\[6pt] &= x(x^2 -tx -x +t ) \\[6pt] &= x^3 - tx^2 - x^2 + tx ,\\[6pt] f ' (x) &= 3x^2 - 2tx - 2x + t ,\\[6pt] f ' \left( - \frac{1}{4} \right) &= \frac{3}{16} + \frac{1}{2} t + \frac{2}{4} +t = -\frac{1}{4} \end{aligned}\] 이므로 \[3+8t+8+16t = -4\] 이다. 이 방정식을 풀면 \(t = - \frac{5}{8}\)이다. 이 값을 사용하여 \(f ' ( \frac{1}{4} )\)을 구하면 \[\begin{aligned} f ' \left( \frac{1}{4} \right) &= \frac{3}{16} + 2 \times \frac{5}{8} \times \frac{1}{4} - 2 \times \frac{1}{4} - \frac{5}{8} \\[6pt] &= \frac{3}{16} + \frac{5}{16} - \frac{8}{16} - \frac{10}{16} = - \frac{5}{8} < 0 \end{aligned}\] 이므로, 문제의 조건을 만족시킨다. 이어서 \(f(8)\)의 값을 구하면 \[f(8) = 8 \times 7 \times \left( 8 + \frac{5}{8} \right) = 8 \times 7 \times \frac{69}{8} = 483\]이다.
(2) 두 번째는 방정식 \(f(x)=0\)의 근이 \(x=-1 ,\) \(x=0,\) \(x=s\)이고, \(0 \le s \le 1\)인 경우이다. \[\begin{aligned} f(x) &= x(x+1)(x-s) \\[6pt] &= x(x^2 +x-sx-s ) \\[6pt] &= x^3 +x^2 -sx^2 -sx ,\\[6pt] f ' (x) &= 3x^2 +2x -2sx -s , \\[6pt] f ' \left( -\frac{1}{4} \right) &= \frac{3}{16} - \frac{1}{2} + \frac{1}{2} s -s = - \frac{1}{4} \end{aligned}\] 이다. 마지막 식을 \(s\)에 대하여 풀면 \[\begin{gathered} 3-8-8s = -4 ,\\[6pt] -8s = 1 ,\\[6pt] s = -\frac{1}{8} \end{gathered}\] 이므로 \(s \ge 0\)이라는 조건에 맞지 않는다. 그러므로 두 번째 경우는 문제의 조건을 만족시키는 함수 \(f(x)\)를 얻지 못한다.
따라서 \(f(8) = 483\)이 유일한 답이다.