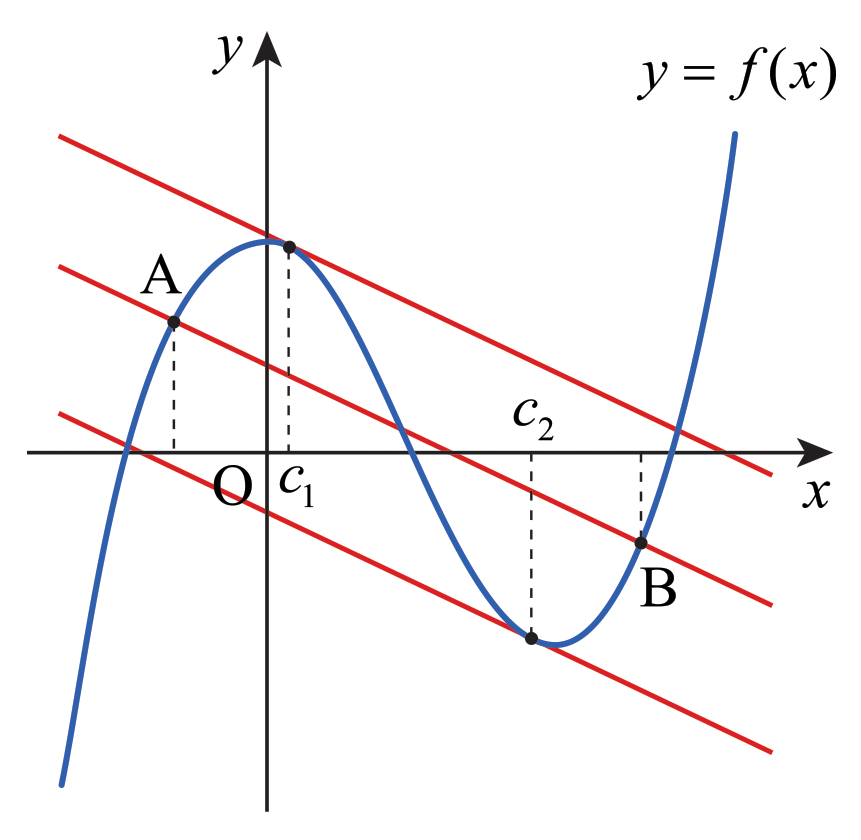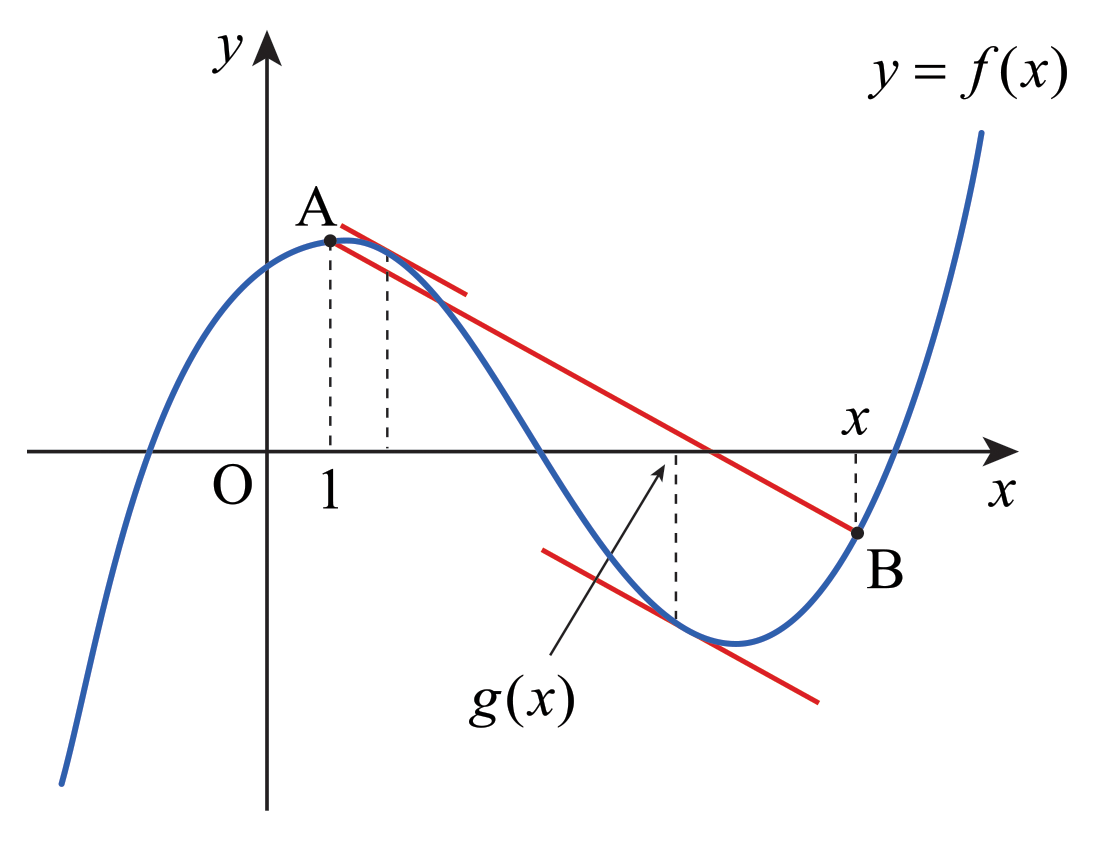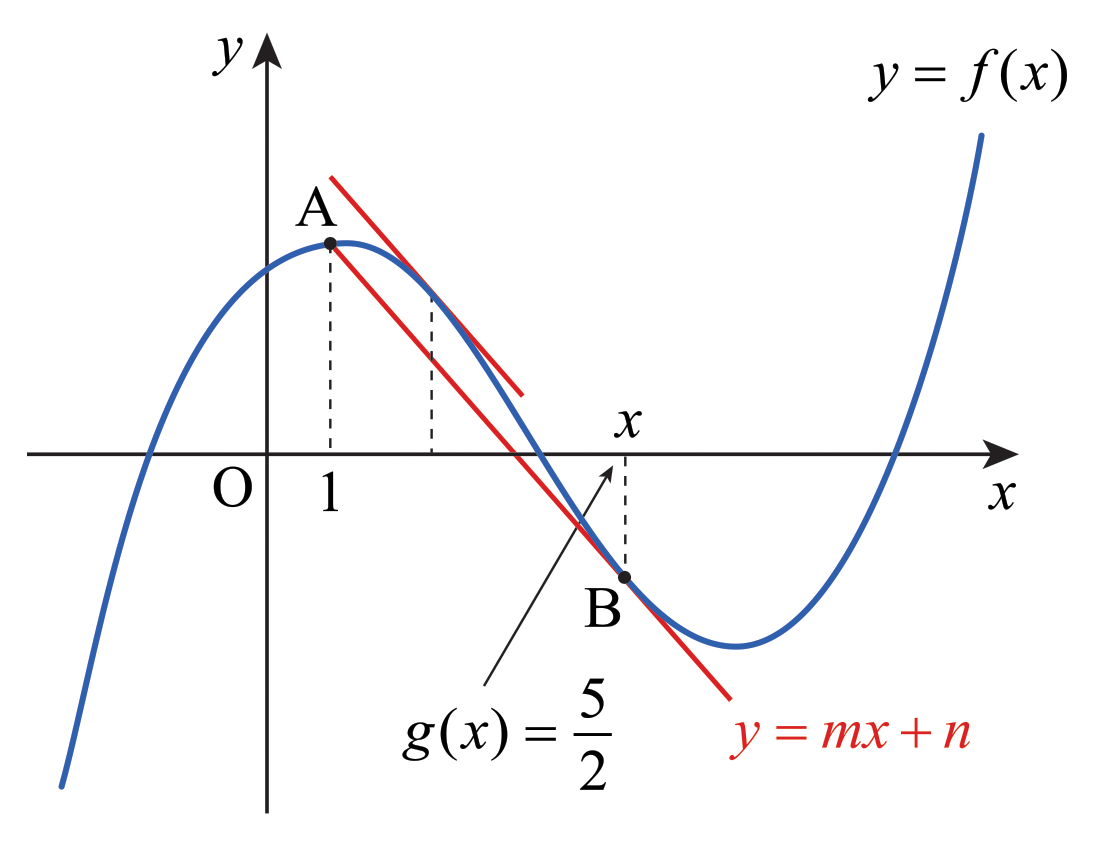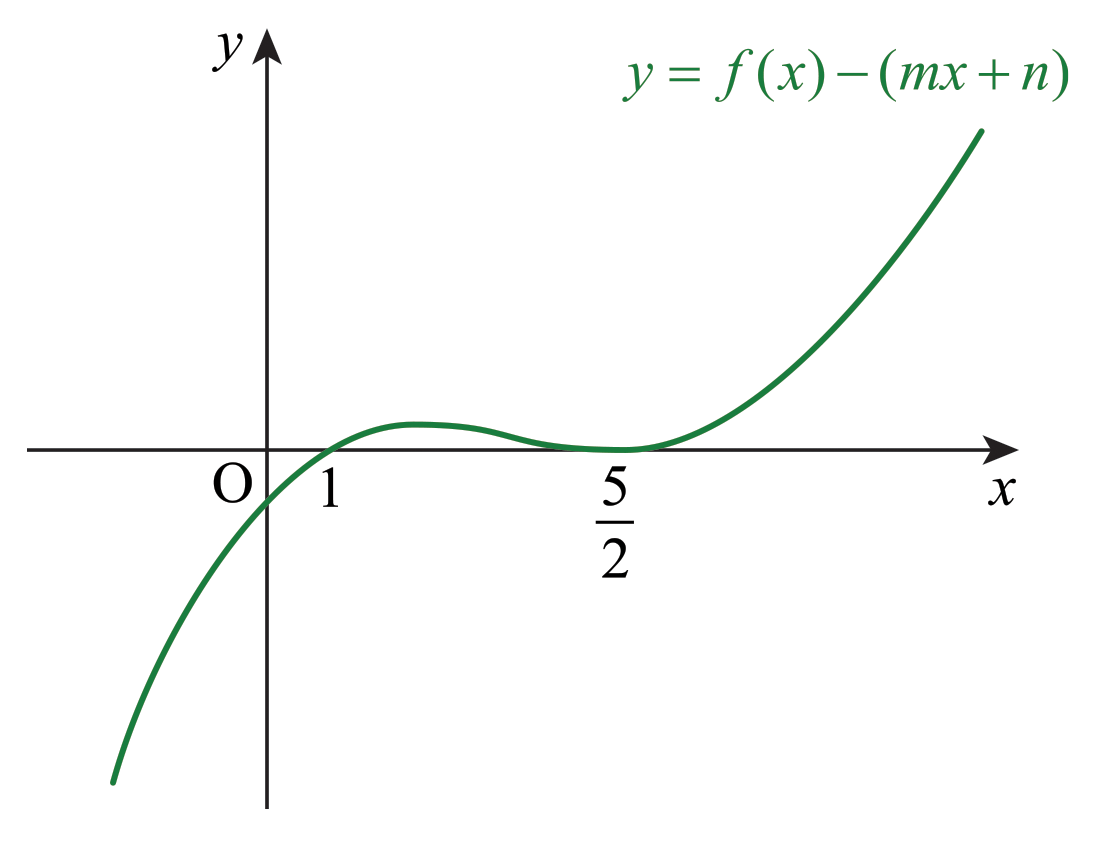2023 수능 수학 공통과목 단답형 문항(16-22번) 풀이

풀이

문제의 방정식을 변형하면 \[\log_2 (3x+2) = \log_2 2^2 + \log_2 (x-2)\] 즉 \[\log_2 (3x+2) = \log_2 (4(x-2))\] 이다. 여기서 로그함수는 일대일 함수이므로 위 등식의 성립하기 위한 필요충분조건은 \[3x+2 = 4(x-2)\] 가 성립하는 것이다. (단, \(3x+2 > 0,\) \(x-2 > 0.\)) 이 방정식을 풀면 \(x=10\)이다.

풀이

\(f ' (x)\)의 역도함수를 구하면 \[f(x) = x^4 -x^2 + k\] 이다. 단, 여기서 \(k\)는 상수이다. 이 식에 \(x=0\)을 대입하면 \[f(0) = k = 3\] 이다. 그러므로 \[f(x) = x^4 - x^2 + 3\] 이고 \[f(2) = 2^4 - 2^2 + 3 = 16 - 4 + 3 = 15\] 이다.

풀이

\[A = \sum_{k=1}^{5} a_k ,\quad B = \sum_{k=1}^{5} b_k\] 라고 하자. 그러면 \[\sum_{k=1}^{5} (3a_k + 5) = 3\sum_{k=1}^{5} a_k + \sum_{k=1}^{5} 5 = 3A+25 = 55\] 이므로 \(A= 10\)이다. 또한 \[\sum_{k=1}^{5} (a_k + b_k) = A+B = 32\] 이므로 \(B=22\)이다. 그러므로 \[\sum_{k=1}^{5} b_k = 22\] 이다.

풀이

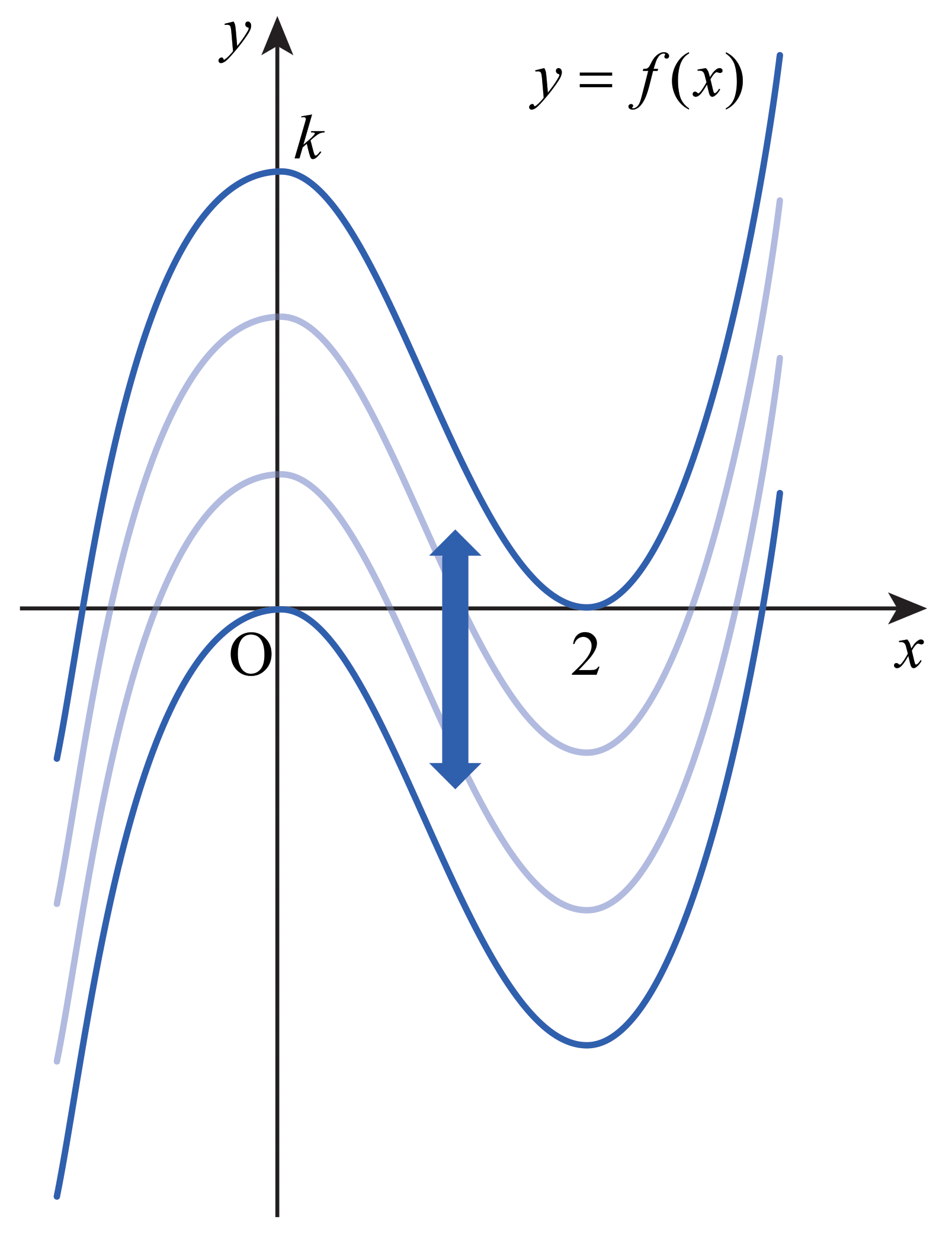
\(f(x) = 2x^3 - 6x^2 + k\)라고 하고 \(f\)의 도함수를 구하면 다음과 같다. \[ f ' (x) = 6x^2 - 12x = 6x(x-2)\] 특히 \(x < 0\)일 때와 \(x > 2\)일 때 \(f ' (x) > 0\)이고, \(0 < x < 2\)일 때 \(f ' (x) < 0\)이므로, \(f\)는 \(x=0\)에서 극댓값을 갖고 \(x=2\)에서 극솟값을 가진다. 따라서 함수 \(y=f(x)\)의 그래프는 다음과 같다. (\(k\)의 값에 따라 그래프가 \(y\)축 방향으로 평행이동한다.)

그래프가 \(y\)축과 만나는 점의 \(y\)좌표가 \(k\)이다. 그러므로 \(k\)의 값이 \(0\)보다 \(x > 0\)의 범위에서 그래프가 \(x\)축과 두 점에서 만날 수 있다. 또한 \(x=2\)일 때 함숫값이 \(0\)보다 작아야 \(x > 0\)의 범위에서 그래프가 \(x\)축과 두 점에서 만날 수 있다. 그러므로 \[f(2) = 16-24+k < 0\] 즉 \(k < 8\)이어야 한다. 따라서 문제의 조건을 만족시키는 \(k\)의 범위는 \(0 < k < 8\)이며, 이 범위에 있는 정수의 개수는 \(7\)이다.

풀이

\(0\le t\le 2\)일 때 \[v(t) = 2t^3 - 8t = 2t(t-2)(t+2)\] 이므로 \(0\le t\le 2\)의 범위에서 \(v(t) \le 0\)이고 \(v(2) =0\)이다.

한편 \(t \ge 2\)일 때 \(v(t)\)는 \(a(t)\)의 역도함수이므로 \[v(t) = 3t^2 + 4t +k\] 이다. (단, 여기서 \(k\)는 상수이다.) 이 식은 \(t=2\)일 때에도 유효하므로 \[v(2) = 12+8+k = 0\] 즉 \(k=-20\)이다. 따라서 \(t \ge 2\)일 때 \[v(t) = 3t^2 + 4t - 20 = (3t+10)(t-2)\] 이며, \(t \ge 2\)일 때 \(v(t) \ge 0\)이다.

그러므로 \(t=0\)에서 \(t=3\)까지 점 \(\mathrm{P}\)가 움직인 거리 \(s\)는 다음과 같다. \[\begin{aligned} s &= \int_{0}^{3} \lvert v(t) \rvert dt \\[6pt] &= -\int_{0}^{2} v(t) dt + \int_{2}^{3} v(t) dt \\[6pt] &= -\int_{0}^{2} (2t^3 -8t ) dt + \int_{2}^{3} (3t^2 + 4t - 20)dt \\[6pt] &= - \left[ \frac{1}{2} t^4 - 4t^2 \right]_{0}^{2} + \left[ t^3 + 2t^2 - 20t \right]_{2}^{3} \\[6pt] &= -(8 - 16) + (27 + 18 - 60 - 8 - 8 + 40) = 17. \end{aligned}\]

풀이

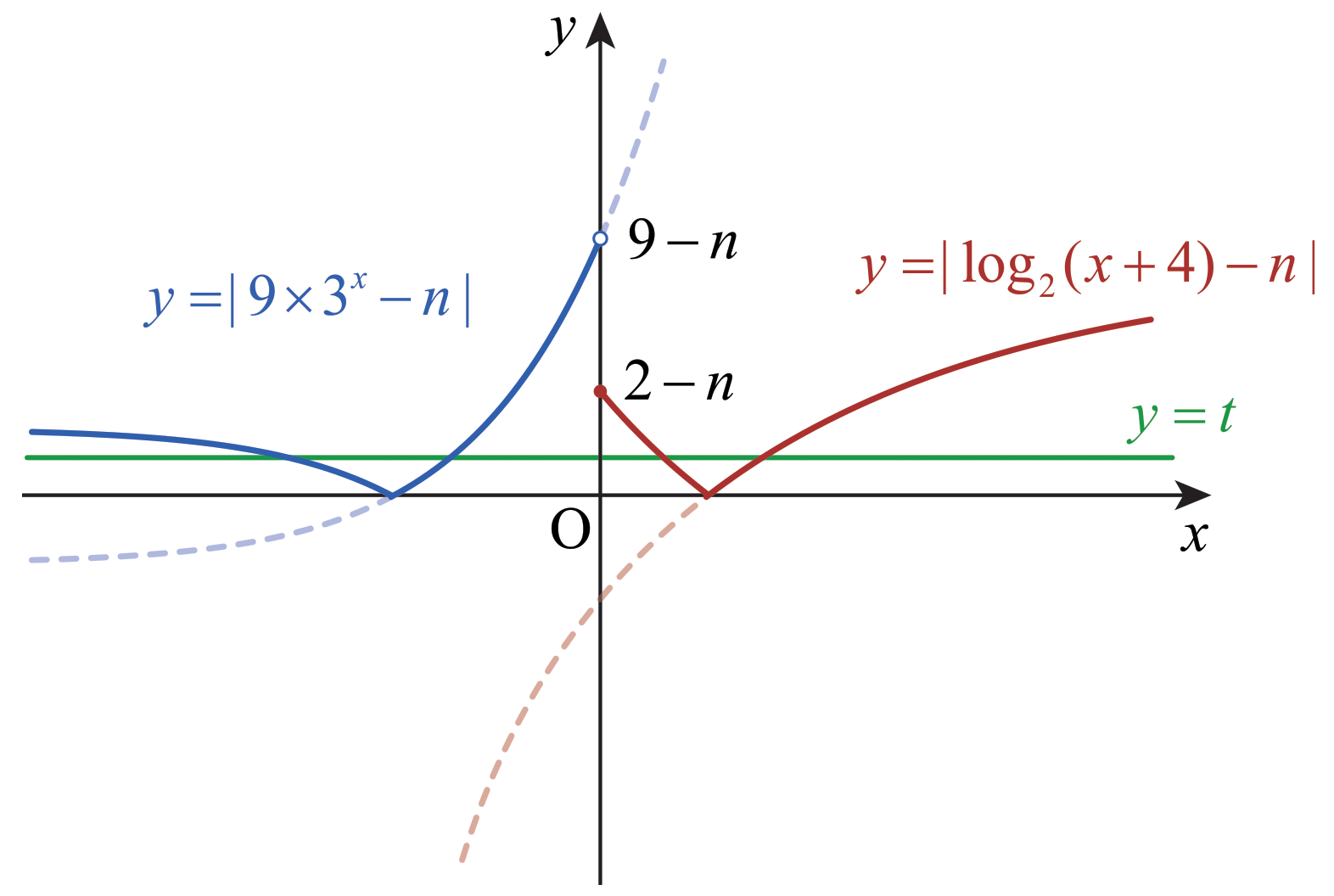
이 문제는 그래프를 그리면 쉽게 풀린다. \(x < 0\)일 때 \[f(x) = \lvert 3^{x+2} -n \rvert = \lvert 9 \times 3^x - n \rvert\] 이고, \(x \ge 0\)일 때 \[f(x) = \lvert \log_2 (x+4) -n \rvert\] 이므로, 그래프를 그리면 다음과 같다.

여기서 \(9-n > 0\)이면 \(x < 0\)인 범위에서 \(f(x) = 0\)일 때가 존재하고, \(2-n < 0\)이면 \(x > 0\)인 범위에서 \(f(x) = 0\)일 때가 존재한다. 이때 \(t\)를 충분히 작은 양수로 정하면 \(x\)에 대한 방정식 \(f(x) = t\)의 서로 다른 실근의 개수가 \(4\)가 된다. 또한 \(f(x) = t\)의 서로 다른 실근의 개수는 \(4\)를 넘을 수 없다.

\(9-n > 0\)과 \(2-n < 0\)을 모두 만족시키는 정수 \(n\)은 \[3 ,\,\, 4 ,\,\, 5 ,\,\, 6 ,\,\, 7 ,\,\, 8\] 이며, 이 값을 모두 더하면 \(33\)이다.

풀이

먼저 삼차함수의 그래프의 특징 하나를 살펴보자. \(f\)가 삼차함수일 때 \(y=f(x)\)의 그래프 위에서 서로 다른 두 점 \(\mathrm{A},\) \(\mathrm{B}\)를 잡은 뒤 직선 \(\mathrm{AB}\)를 그으면, 미분계수가 직선 \(\mathrm{AB}\)의 기울기와 같아지는 점이 딱 두 개 존재한다. 아래 그림에서는 \(x=c_1\)과 \(x=c_2\)가 그와 같은 점이다.

이제 문제를 풀어 보자. [1]의 조건을 사용하면 \(x\ne 1\)일 때 \[\frac{f(x)-f(1)}{x-1} = f ' (g(x))\] 가 성립한다. 여기서 좌변은 \(f\)의 그래프 위의 두 점 \((1,\,f(1))\)과 \((x,\,f(x))\)를 지나는 직선의 기울기이며, 우변은 \(g(x)\)에서 \(f\)의 미분계수이다. 앞에서 밝힌 바와 같이 \(x\ne 1\)일 때 \[\frac{f(x)-f(1)}{x-1} = f ' (c) \tag{1}\] 인 점 \(c\)는 두 개가 존재한다. 아래 그림을 보자.

그러한 점 \(c\) 중 큰 값을 \(g(x)\)의 값으로 정하자. 만약 그러한 점 \(c\) 중 작은 값을 정하면 \(x\)가 무한히 작아질 때 직선의 기울기가 무한히 작아지므로 \(g(x)\)의 값도 무한히 작아지는데, 그러면 조건 [2]에서 \(g\)가 최솟값을 갖는다는 사실에 모순이기 때문이다. 더욱이 \(g(x)\)는 등식 (1)을 만족시키는 두 개의 값 \(c\) 중에서 더 큰 값하고만 일치하든지 또는 더 작은 값하고만 일치한다. 왜냐하면, \(g(x)\)가 두 개의 값 \(c\) 중 더 큰 값과 일치하는 경우와 더 작은 값과 일차하는 경우가 모두 존재한다면 \(g\)가 연속이라는 조건에 모순이기 때문이다.

아래 그림과 같이 점 \(\mathrm{B}\)가 직선 \(\mathrm{AB}\)의 접점이 될 때 \(g\)의 값이 최소가 된다.

이때 직선 \(\mathrm{AB}\)의 방정식을 \(y=mx+n\)이라고 하자. 그러면 \(y=f(x)-(mx+n)\)의 그래프는 아래 그림과 같다.

그러므로 \[f(x)-(mx+n) = (x-1)\left( x- \frac{5}{2} \right)^2\] 이라고 쓸 수 있고, \[f(x) = (x-1)\left( x- \frac{5}{2}\right)^2 + mx+n\tag{2}\] 이라고 쓸 수 있다. 여기서 \(m\)의 값과 \(n\)의 값을 구하자.

조건 [3]에서 \(f(0)=-3\)이므로 \[f(0) = (-1)\times \frac{25}{4} +n =-3\] 즉 \[n = -3 + \frac{25}{4} = \frac{13}{4}\tag{3}\] 이다. 또한 \[f ' (x) = \left( x- \frac{5}{2}\right)^2 + 2(x-1)\left( x- \frac{5}{2}\right) +m\] 이므로 \[f '(1) = \frac{9}{4} +m\] 이다. 그런데 \(g\)와 \(f ' \)이 모두 연속함수이므로 \[f ' (1) = \lim_{x\rightarrow 1}\frac{f(x)-f(1)}{x-1} = \lim_{x\rightarrow 1} f ' ( g(x)) = f ' (g(1))\] 이다. [여기서 \(g(1) \ne 1\)임에 주의하자. 어차피 \(g\)의 최솟값은 \(\frac{5}{2}\)라는ㅜㅜ \(f'\)이 이차함수이므로 일대일 함수가 아니다.] \[\begin{aligned} f ' ' (x) &= 2\left( x-\frac{5}{2}\right) + 2 \left(x-\frac{5}{2}\right) + 2(x-1) \\[6pt] &= 2x-5+2x-5+2x-2 \\[6pt] &= 6x- 12 = 6(x-2) \end{aligned}\] 이므로 \((2,\,f(2))\)가 \(y=f(x)\)의 그래프의 변곡점이다. 삼차함수의 그래프는 변곡점에 대하여 점대칭이므로 \[f ' (1) = f ' (3)\] 이다. 또한 미분계수가 \(f '(1)\)과 같은 것은 \(x=3\)일 때뿐이다. [\(f ' \)이 이차함수이기 때문이다.] 그러므로 \(g(1) = 3\)이다. 따라서 조건 [3]에 의하여 \[f(3) = f(g(1)) = 6\] 이며, 이 값을 (2)에 대입하여 \(n\)의 값을 구하고 \(f(x)\)의 식을 완성하면 \[f(x) = (x-1)\left( x - \frac{5}{2} \right)^2 + \frac{3}{4} x + \frac{13}{4}\] 이다. 따라서 \[f(4) = 3 \times \frac{9}{4} + 3 + \frac{13}{4} = 13\] 이다.